최초입문 6강 part 2 (2023. 1. 17)

 

Attribute VOP, Attribute Wrangle 기본이해와 비교

VEX

후디니에서 수학을 알아야하는 이유: 램프 만들기

램프 만들기 아이디어, if A와 B가 같을 때

If A와 B가 다를 때, 램프 컨셉 다지기

램프 뼈대 만들기

램프 면 작업하기

FX와 IK에 대하여

 

과제:

램프 만들기

-좌표 값은 base와 target에만 입력

-target이 멀어질수록 head의 관심이 줄어든다.

-target이 가까우면 일정 거리를 두고 비춘다.

 

6강 part 2

Attribute VOP

Attribute와 변수의 공통점

- 공통점: VEX계산과 연산 과정에서 값을 저장하고 연산 중에 그 값을 다시 이용할 수 있다.

- 차이점: Attribute는 결과에 저장되며 다음 노드에서도 다시 이용이 가능하지만, 변수는 현재 노드에서만 이용할 수 있다.

 

방법의 차이일 뿐, 결과는 똑같다

 

 

Attribute Wrangle: Math(VEX) style

- 확정적 명령

- 변수가 고정되어 있다.

 

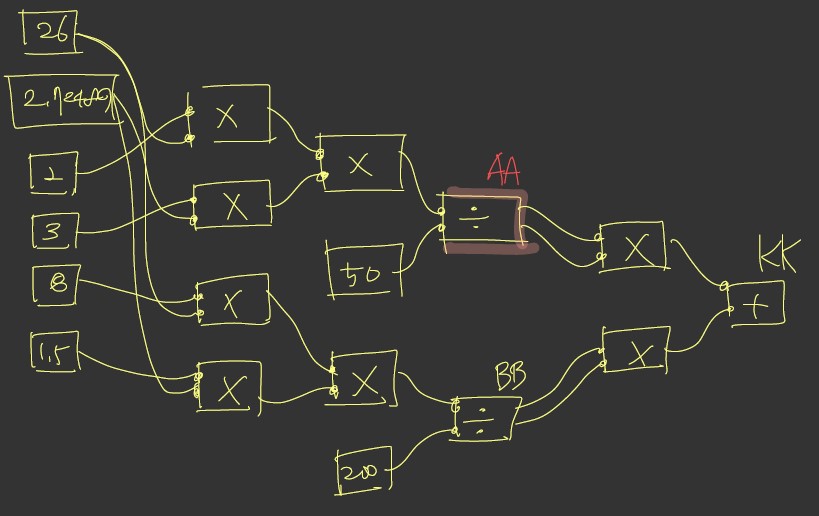
Q. KK의 값을 구하시오.

a = 26

b = 2.72489

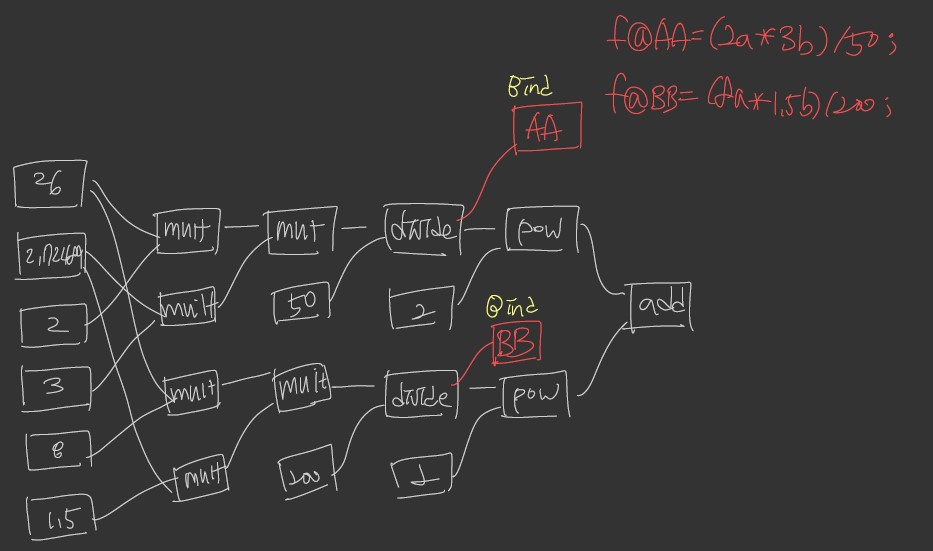
AA = (2a * 3b) / 50

BB = (8a * 1.5b) / 200

KK = (AA)2 + (BB)2

 

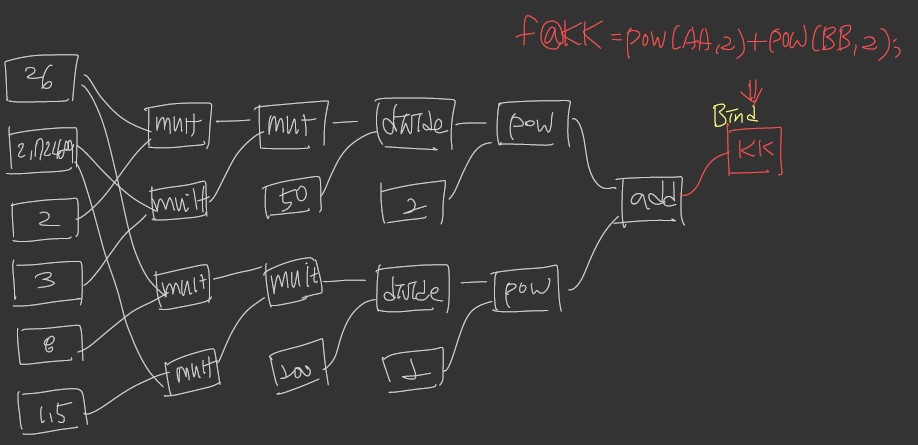
with VEX: 복잡한 연산에서 더 큰 기능을 발휘한다.

float a = 26;

float b = 2.2489;

float AA = (2a * 3b)/50;

float BB = (8a * 1.5b)/200;

f@KK = pow(AA, 2) + pow(BB, 2);

 

VOP style

- 유동적 명령

- 모든 노드가 변수로서 역할을 한다.

 

01

횡으로 나열되는 VOP

 

 

값

- 노드는 VEX가 지원하는 data type의 정보를 가지고 있다면 그자체로 값의 기능을 한다.

 

input과 output이 있다

 

 

- add노드에 들어오는 정보의 순서는 중요하다.

- 먼저 들어온 정보: 1번 input

- 2번째 들어온 정보: 2번 input

- add노드 = 1번 + 2번

 

- 연산의 앞순서에 있는 data type을 결과값이 따라가므로 연결되는 와이어의 순서는 매우 중요하다.

 

연산의 순서와 노드 input의 순서

 

 

012

Wrangle ➡ 수식으로 표현 ➡ VOP

 

 

VOP에서의 Attribute

- type casting에 차이가 있다.

- VOP에서 Attribute를 사용하기 위해 bind, bind export 노드를 활용한다. 

- Attribute로 만들고 싶은 노드에 연결

 

01

VOP에서 Attibute 만들기

 

 

in HOUDINI

- 인터페이스 레이아웃 수정하고 씬뷰와 네트워크 뷰에 링크 걸기: 1번

 

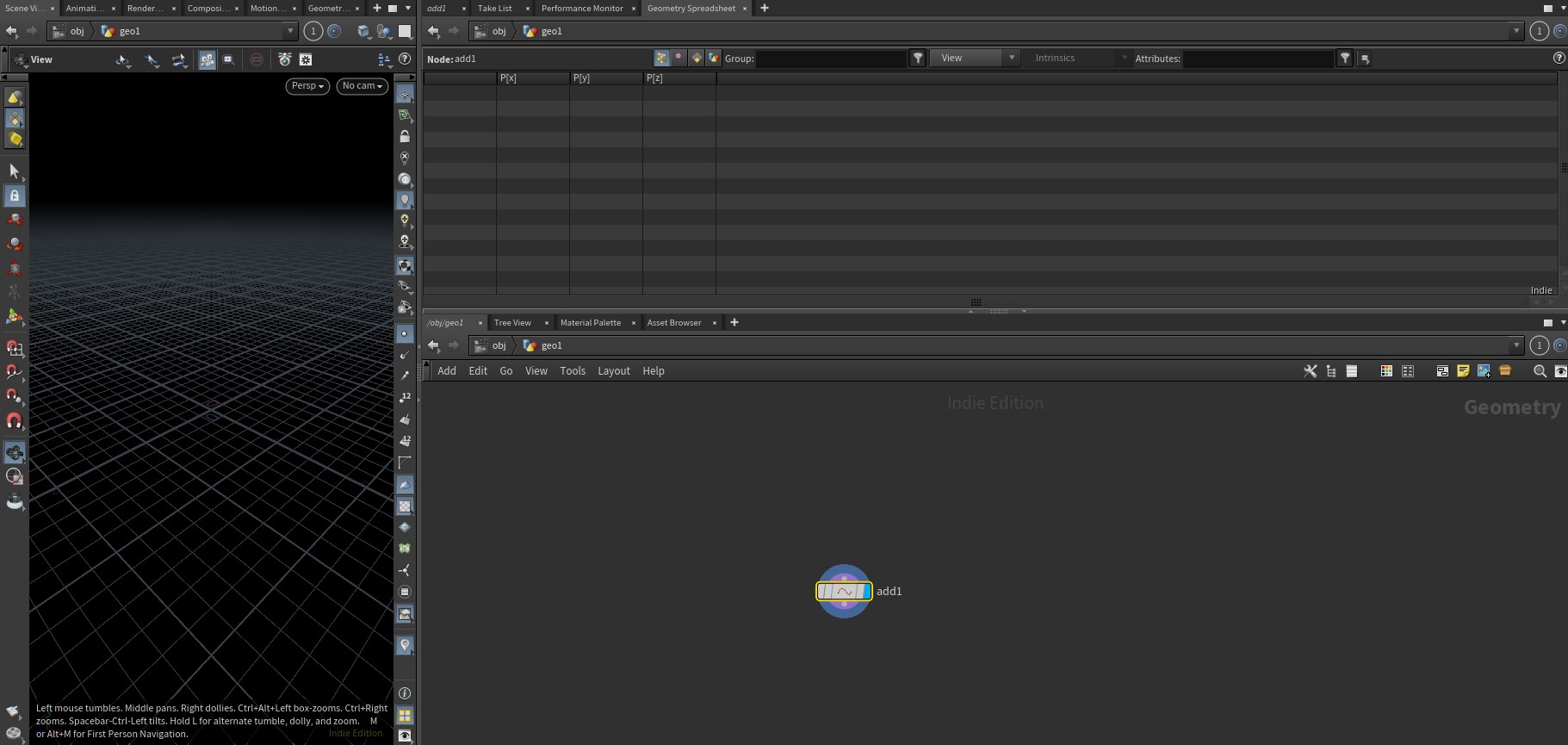
각 화면의 링크 고정

 

 

- Add 노드에 point 생성하고 Attribute VOP 연결, Geometry Spreadsheet에서 확인

 

01

Attribute Wrangle과 Attribute VOP 파라미터 차이 (Run Over 옵션 중요)

 

 

- Attribute VOP을 클릭해서 VEX Builder로 들어간다.

- 들어갔을 때 있는 2개의 노드는 편의를 위해 미리 세팅된 노드는 연습을 위해 지우고 시작한다.

 

1. 작업을 위해 Attribute을 불러오는 법

2. 상수는 만드는 법

3. 연산자를 꺼내는 법

4. 값을 분해 했다가 뭉치는 법

5. 값을 Attribute로 출력하는 법

 

bind 노드 활용

- Attribute VOP 노드의 input으로 들어와 이용할 수 있는 Attribute이 있다면 그것을 사용한다.

- Attribute VOP안에서 bind 노드 생성

binde 파라미터

 

 

- Name: 우리가 이용할 수 있는 Attribute가 있다면 그것을 이용하겠다.

- 현재 존재하는 parm(parameter) Attribute는 Add의 info에서 확인할 수 없는 Attribute이다.

- 우리가 알고 있는 Attribute인 P(position)을 넣고, [Type: 3Floats(vector)]

 

@P 세팅 완료

 

 

- 상수를 만들어주는 Constant 노드 생성

- [Constant Type]은 data type

- [Constant Type: Vector(vector)]로 설정하고 임의의 값 입력

 

- 또다른 Constant 노드 생성

- [Constant Type: Float(float)]으로 설정하고 임의의 값 입력

 

- 연산자 노드: add, multiply

- 연산자 노드를 생성하고 Constant와 연결하면 input 노드가 추가된다.

 

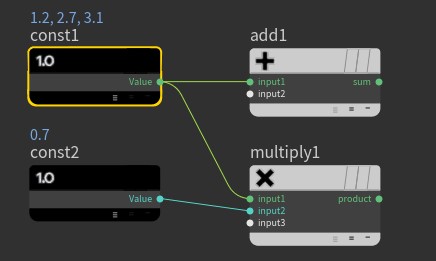
vector 값인 const1 + (const1 * float 값인 const2)

 

 

- 변수이기 때문에 계산은 완료하였지만 Geometry Spreadsheet에서 확인할 수 없다.

 

bind export 노드로 결과값 출력

- input이 없는 bind 노드와 다르게 bind export 노드는 input이 존재한다.

- Attribute Name을 정해주면, Geometry Spreadsheet에 Attribute가 생긴 것을 확인할 수 있다.

 

- Vector to Float: vector를 float으로 바꾸는 노드

- Float to Vector: float를 모아 vector로 바꾸는 노드

 

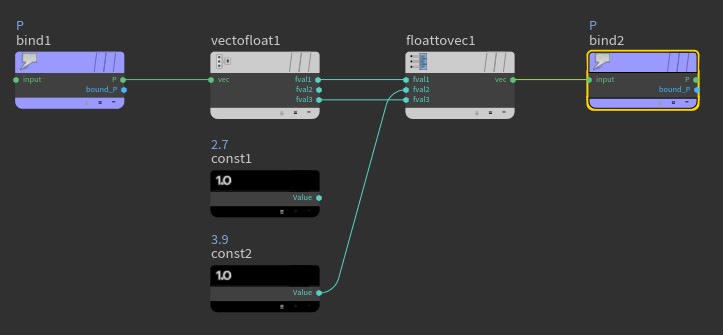
01

원래 주어진 vector의 y값이무시되고 전부 0이 된다.

 

 

예제1

- bind 노드를 이용해 point attribute를 불러온다.

- Name: P

- Type: 3Floats (vector)

 

- Constant 노드 생성하고 값 입력 (변수의 이름을 구체적으로 설정할 필요는 없다.)

 

float = CC;

CC = 2.7;

 

변수 CC

 

 

float = DD;

DD = 3.9;

 

변수 DD

 

 

@P.y = DD;

 

01

bind export로 결과값 출력

 

 

f@AA;

@AA = 2.7;

 

f@BB;

@BB = 3.9;

 

@P.y = @BB;

 

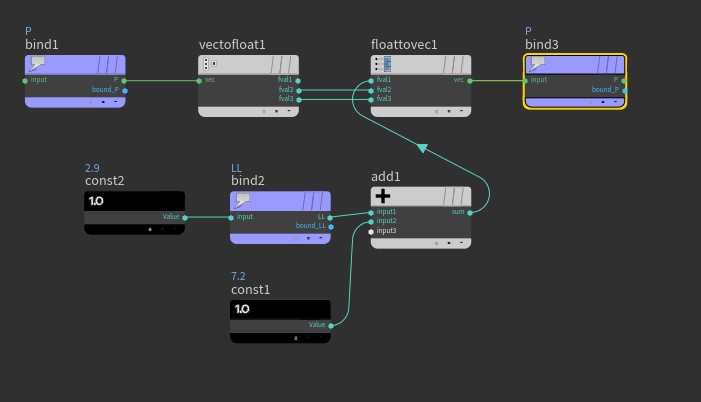
01

@P.y를 Attribute VOP로 나타내기

 

 

예제2

- bind 노드 생성

- Name: P

- Type: Vector (vector), 3Floats Vector (vector)와 차이 없다.

 

float KK;

f@LL;

 

01

변수 KK와 Attribute LL

 

 

KK = 7.2;

@LL = 2.9;

 

변수 KK와 Attribute LL 값

 

 

@P.x = @LL + KK;

 

012

@P.x의 Attirbute VOP 과정

 

 

 

예제3

f@TWA = 0.7;

float TWB = 0.4;

 

변수 TWB와 Attribute TWA

 

 

f@TWC = (@TWA * 2) + (TWB * 0.7);

 

01

Attribute TWC의 Attribute VOP 과정

 

 

예제4

vector home;

vector away;

 

home = set(0, 2, 0);

away = set(3, 1, 2);

 

vector 상수

 

 

v@Dir;

@Dir = away – home;

 

01

Attribute Dir의 Attribute VOP 처리 과정

 

 

예제5

v@home = set(0.5, 0.9, -0.3);

v@away = set(-4, -4, 6.2);

 

01

vector Attribute인 home과  away

 

 

v@Dir = (@away - @home) * 0.5;

 

v@Dir의 Attribute VOP 처리 과정

 

 

f@power = length(@Dir);

 

Attribute VOP에서 length 노드를 사용하여 Attirbute power를 나타낸다

 

 

예제6

@P.x = @P.x + 1;

 

기본 제공 노드를 활용하여 @P값 추출

 

 

예제7

@P.x = @P.x + @Frame;

 

기본 제공 노드에 있는 @Frame 을 활용

 

 

예제8

v@Dir = set(@Frame, (@Frame / 2), 0);

 

그리고 연산 노드를 연결한다

 

 

@P = @P + @Dir;

 

기본 제공 노드로 export된 결과 값

 

 

예제9

vector VEL = set(1.0, 0.5, 0.3);

float Divide = 20;

float TT = @Frame;

@P = @P + (VEL / Divide) * TT;

 

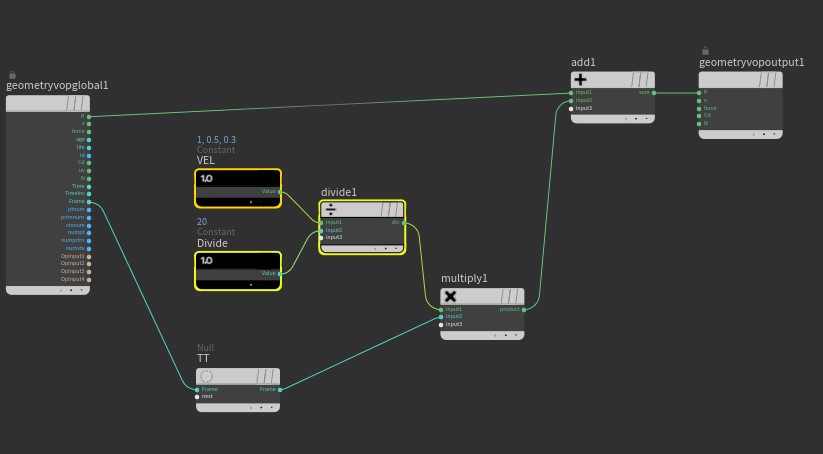
Attirbute VOP는 노드를 활용하는 직관적인 방법인 것 같다